 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
若α1,···,αn是Rn的一组标准正交基,A是n阶正交矩阵,证明:Aα1,Aα2,···,Aαn是Rn的一组标准正交基。
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“若α1,···,αn是Rn的一组标准正交基,A是n阶正交矩阵…”相关的问题
更多“若α1,···,αn是Rn的一组标准正交基,A是n阶正交矩阵…”相关的问题
设V是对于非退化对称双线性函数f(α,β)的n维准欧氏空间,V的一组基ε1,...,εn如果满足
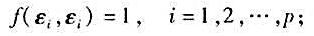
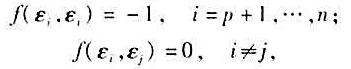
则称为V的一组正交基。如果V上的线性变换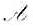 满足
满足
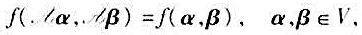
则称 为V的一个准正交变换。试证:
为V的一个准正交变换。试证:
1)准正交变换是可逆的,且逆变换也是准正交变换;
2)准正交变换的乘积仍是准正交变换;
3)准正交变换 的特征向量α,若满足f(α,α)≠0,则其特征值等于1或-1;
的特征向量α,若满足f(α,α)≠0,则其特征值等于1或-1;
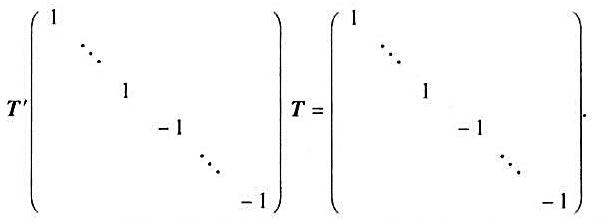
4)准正交变换在正交基下的矩阵T满足
欧氏空间V中的线性变换 称为反称的,如果对任意,α,β∈V,
称为反称的,如果对任意,α,β∈V,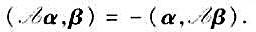 证明:
证明:
1) 为反称的充分必要条件是,
为反称的充分必要条件是, 在一组标准正交基下的矩阵为反称的;
在一组标准正交基下的矩阵为反称的;
2)如果V1是反称线性变换的 不变子空间,则
不变子空间,则 也是。
也是。
设二次型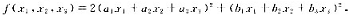 记a=
记a=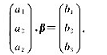
(1)证明二元型f对应的矩阵为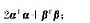
(2)若α、β正交且均为单位向量,证明二次型/在正交变换下的标准形为二次型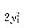
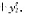
证明实系数线性方程组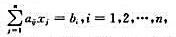 有解的充要条件是向量β=(b1,b2,···,bn)∈Rn与齐次线性方程组
有解的充要条件是向量β=(b1,b2,···,bn)∈Rn与齐次线性方程组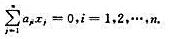 的解空间正交。
的解空间正交。
设f(x1,x2,···,xn)=X'AX是一实二次型,λ1,λ2,···,λn是A的特征多项式的根,且λ1≤λ2≤···≤λn。证明:对任一X∈Rn,有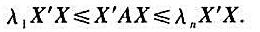
证明:设A,B都是n阶正交方阵,则
(1)|A|=1或-1(2)AT,A-1,AB也是正交方阵。
(2) A正交方阵,得ATA=E,由AAT=E得AT正交方阵。又A-1=AT, 故A-1正交方阵。A,B是n阶正交矩阵,故A-1=AT,B-1=BT。(AB)T(AB) =BTATAB=B-1A-1AB=E, 故AB也是正交方阵。