 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
适当选取坐标系,求下列轨迹方程.(1)到两定点距离之差等于常数的点的轨迹;(2)到一定点和一一个定平面(定点不在定平面上)距离之比等于常数的点的轨迹;(3)设有一个定平面和垂直于它的一条定直线,求到定平面与到定直线的距离相等的点的轨迹;(4)求与两给定直线等距离的点的轨迹,已知两直线之间的距离为a,夹角为α.
适当选取坐标系,求下列轨迹方程.(1)到两定点距离之差等于常数的点的轨迹;(2)到一定点和一一个定平面(定点不在定平面上)距离之比等于常数的点的轨迹;(3)设有一个定平面和垂直于它的一条定直线,求到定平面与到定直线的距离相等的点的轨迹;(4)求与两给定直线等距离的点的轨迹,已知两直线之间的距离为a,夹角为α.
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案


 更多“适当选取坐标系,求下列轨迹方程.(1)到两定点距离之差等于常…”相关的问题
更多“适当选取坐标系,求下列轨迹方程.(1)到两定点距离之差等于常…”相关的问题
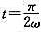 时的速度和加速度。
时的速度和加速度。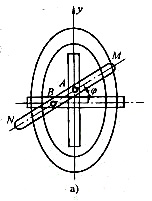
 ,原点不动,得坐标系
,原点不动,得坐标系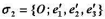 ,求σ1到σ2的点的坐标变换公式.
,求σ1到σ2的点的坐标变换公式.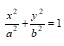 ,加速度恒与y轴平行。当t=0时的初始坐标(0,b),初速度为v0,求质点在轨迹上任何位置时所受的力。
,加速度恒与y轴平行。当t=0时的初始坐标(0,b),初速度为v0,求质点在轨迹上任何位置时所受的力。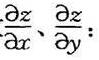
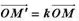 ,其中,常数k>0,则称τ是同位相似(或相似),称O为位似中心,k称为位似系数.
,其中,常数k>0,则称τ是同位相似(或相似),称O为位似中心,k称为位似系数.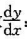 :
:















